线性代数：矩阵

方程组的几何解释

矩阵的发明是为了用一种简洁的方式表达线性方程组。对于一个方程组，如 $$\left{\begin{align*}2x - y = 0\ -x + 2y = 3\end{align*}\right.$$ ，可以写成矩阵和未知量相乘（$$ A \mathbf x = \mathbf b $$）的形式：

$\begin{bmatrix}2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix}x \\ y \end{bmatrix} = \begin{bmatrix}0 \\ 3 \end{bmatrix}$

矩阵分为行（row）和列（column）。

对于这个矩阵，可以画出它的行图像（Row picture）：

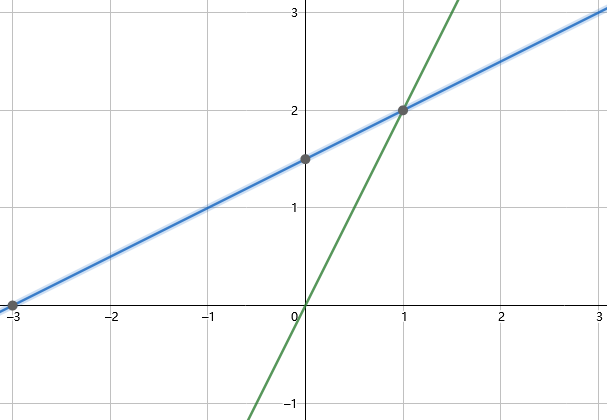
列图像（Column picture）则关注列的部分。

$x\begin{bmatrix}2 \\ -1\end{bmatrix} + y\begin{bmatrix}-1 \\ 2 \end{bmatrix} = \begin{bmatrix}0 \\ 3 \end{bmatrix}$

这样问题就转化成一个列的线性组合（Linear combination of columns）。那么我们要求的就是：在坐标系下，$x$ 和 $y$ 分别取何值时这两个向量相加得到 $(0, 3)$，也就是使得 $A\mathbf x = \mathbf b$. 并且，当 $\mathbf x$ 向量任取时，便可以得到 $xy$ 平面（plane）中的任意向量。

针对三维及更高维的空间，也可以这样表示并计算。

矩阵与向量的计算有两种方式：

1. 将矩阵看成列的线性组合

   $\begin{bmatrix}2 & 5 \\ 1 & 3 \end{bmatrix} \begin{bmatrix}1 \\ 2 \end{bmatrix} = 1\begin{bmatrix}2 \\ 1\end{bmatrix} + 2\begin{bmatrix}5 \\ 3 \end{bmatrix} = \begin{bmatrix}12 \\ 7 \end{bmatrix}$

2. 点乘运算

   $\begin{bmatrix}2 & 5 \\ 1 & 3 \end{bmatrix} \begin{bmatrix}1 \\ 2 \end{bmatrix} = \begin{bmatrix}2*1 + 5 * 2 \\ 1*1 + 3*2\end{bmatrix} = \begin{bmatrix}12 \\ 7 \end{bmatrix}$

   结果中的第1行第1列，是由左侧矩阵第一行和右侧矩阵第1列点乘得到的。其他行列同理。

矩阵可以对行和列进行初等变换。对于行初等变换，有以下3种矩阵运算：

1. 交换任意2行
2. 某一行的元素全部乘以一个非0数
3. 某一行的元素加上另一行对应元素的 N 倍（N 不为0）

消元 Elimination

有一个方程组 $$\left{\begin{align*}x + 2y + z &= 2\ 3x + 8y + z &= 12\ 4y + z &= 2 \end{align*} \right.$$，我们可以写出它的系数矩阵 $A$ 为 $$\begin{bmatrix}1 & 2 & 1 \ 3 & 8 & 1 \ 0 & 4 & 1\end{bmatrix}$$.

接下来是主题——消元。按照 MATLAB 的做法，先对系数矩阵进行处理。首先消除消除非主元行中 $x$ 前面的系数。这里将左上角的 1 称为主元（pivot），第一行称为主元行。保持第一行不变，第二行减去 3 倍的第一行：

$\begin{bmatrix}\boxed 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1\end{bmatrix} \overset{(2,1)}{\Rightarrow} \begin{bmatrix}\boxed 1 & 2 & 1 \\ 0 & \boxed 2 & -2 \\ 0 & 4 & 1\end{bmatrix} \overset{(3,2)}{\Rightarrow} \begin{bmatrix}\boxed 1 & 2 & 1 \\ 0 & \boxed 2 & -2 \\ 0 & 0 & \boxed 5\end{bmatrix}$

第二步：此时方程组中后两个式子只剩下未知数 $y$ 和 $z$。消除第三行中 $y$ 的系数。在这一步中，将中间的 2 作为主元。

最后一步如法炮制，得到一个上三角矩阵（upper triangular），记为 $U$.

在变换时，主元不能为 0，可以通过行变换将其他行放到上面。

得到上三角行列式后，进行回代（Back substitution）。

引入右侧的向量 $\mathbf b$，得到原方程组的增广矩阵（Augmented matrix）：$$\begin{bmatrix}1 & 2 & 1 & 2 \ 3 & 8 & 1 & 12\ 0 & 4 & 1 & 2\end{bmatrix}$$. 对向量 $\mathbf b$ 重复刚才在系数矩阵中进行的各步操作得到 $$\left(\begin{array}{c}2 \ 6\ -10\end{array}\right)$$，记为向量 $\mathbf c$ . 代回方程组 $$\left{\begin{align*}x + 2y + z &= 2\ 2y - z &= 6\ 5z &= 10\end{align*}\right.$$ 便可解得值。

消元矩阵 Elimination matrices

我们可以通过构造一个矩阵，使其与原矩阵相乘，来完成消元的操作，也就是以矩阵运算来描述高斯消元。这有利于理解矩阵的计算。

先考虑单位矩阵（通常记为 $E$ 或 $I$）。一个 3 × 3 的单位矩阵 $\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1\end{bmatrix}$，记为 $E_3$ 或 $I_3$. 同样大小的单位矩阵乘以任何矩阵得到该矩阵本身，即 $AE = EA = A$. （联系矩阵的乘法，思考该式）

• Step1: 从第二行中减去三倍的行一

  考虑单位矩阵：

  $\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1\end{bmatrix} = \begin{bmatrix}1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1\end{bmatrix}$

  为了从第二行中减去三倍行1，观察到元素 $(2, 1)$ 控制运算过程中第一行对第二行的贡献，将其改成 -3 得：

  $\begin{bmatrix}1 & 0 & 0 \\ -3 & 1 & 0\\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1\end{bmatrix} = \begin{bmatrix}1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1\end{bmatrix}$

• Step2: 从第三行中减去两倍的行二

  $\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & -2 & 1\end{bmatrix} \begin{bmatrix}1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1\end{bmatrix} = \begin{bmatrix}1 & 2 & 1 \\ 0 & 2 & -2\\ 0 & 0 & 5\end{bmatrix}$

综上，我们通过矩阵 $E_{21}$ 将后两行 $x$ 的系数消除，又通过 $E_{32}$ 消除了第三行中 $y$ 的系数，得到上三角矩阵 $U$： $E_{32}(E_{21}A) = U$.

矩阵的乘法

矩阵的乘法具有结合律（Associative law）但不符合交换律。对于上一节提到的转换关系，可以将 $E_{32}$ 和 $E_{21}$ 合并为一个矩阵，并把它叫作 $E$。即有 $E_{32}(E_{21}A) = (E_{32}E_{21})A = EA = U$. 矩阵 $E$ 也是几个初等矩阵（Elementary matrix）的积。

矩阵的乘法中，单个元素的值为 元素的角度考虑，$C_{ij} = \prod_{k=1}^N = A_{ik} \times B_{kj}$。此外，还可以用向量的方法计算：

• 从列向量（Column vector）的角度：

  \begin{bmatrix}- & - & - \\ - & - & - \\ - & - & -\end{bmatrix} \begin{bmatrix}3\\ 4\\ 5\end{bmatrix} = \begin{align*}3\times col1 \\ + \\ 4\times col2\\ +\\ 5\times col3\end{align*}

• 从行向量（Row vector）的角度：

  \begin{bmatrix}1 & 2& 7\end{bmatrix} \begin{bmatrix}- & - & - \\ - & - & - \\ - & - & - \end{bmatrix} = \begin{align*} 1\times row1 \\ + \\ 2\times row2\\ +\\ 7\times row3 \end{align*}

• 使用行和列向量计算（$AB = sums\ of\ (cols\ of\ A)\times (rows\ of\ B)$）

  补充一个知识，对于一个 $m\times 1$ 和一个 $1\times p$ 的矩阵相乘，可以得到一个 $m\times p$ 的矩阵，如：

  $\begin{bmatrix}2\ 3\ 4\end{bmatrix}
  \begin{bmatrix}1 & 6\end{bmatrix}

  \begin{bmatrix}2 & 12\ 3 & 18\ 4 & 24\end{bmatrix}$

  那么，对于一个 $3\times 2$ 和一个 $2\times 2$ 的矩阵相乘，可以用不同行列间组合再相加：

  $\begin{bmatrix}2 & 7\\ 3 & 8\\ 4 & 9\end{bmatrix} \begin{bmatrix}1 & 6\\ 0 & 0\end{bmatrix} = \begin{bmatrix}2\\ 3\\ 4\end{bmatrix} \begin{bmatrix}1 & 6\end{bmatrix} + \begin{bmatrix}7\\ 8\\ 9\end{bmatrix} \begin{bmatrix}0 & 0\end{bmatrix} = \begin{bmatrix}2 & 12\\ 3 & 18\\ 4 & 24\end{bmatrix}$

观察结果：所有行都依赖于 $\begin{bmatrix}1 & 6\end{bmatrix}$，如果画出这些行的向量，他们都是同一个方向；此外，所有列都依赖于 $\begin{bmatrix}2\\ 3\\ 4\end{bmatrix}$，所有列向量也都是共线的。

分块乘法 Block multipitation

两个分块矩阵相乘（block multiplication）和元素相乘很相似，可以把每个“块”当一个元素，得到像一般矩阵乘法那样的公式：

$\left[\begin{array}{llll}A_{11} & A_{12} \\ A_{21} & A_{22}\end{array}\right]\left[\begin{array}{lll}B_{11} & B_{12} \\ B_{21} & B_{22}\end{array}\right]=\left[\begin{array}{lll}A_{11} B_{11}+A_{12} B_{21} & A_{11} B_{12}+A_{12} B_{22} \\ A_{21} B_{11}+A_{22} B_{21} & A_{21} B_{12}+A_{22} B_{22}\end{array}\right]$

例如 :

$\left[\begin{array}{llll}1 & 2 & \mid & 3 \\ 4 & 5 & \mid & 6 \\ - & - & - & - \\ 7 & 8 & \mid & 9\end{array}\right]\left[\begin{array}{lll}1 & \mid & 2 \\ 3 & \mid & 4 \\ - & - & - \\ 5 & \mid & 6\end{array}\right] = \left[\begin{array}{ll}{\left[\begin{array}{ll}1 & 2 \\ 4 & 5\end{array}\right]\left[\begin{array}{l}1 \\ 3\end{array}\right]+\left[\begin{array}{l}3 \\ 6\end{array}\right][5]} & {\left[\begin{array}{ll}1 & 2 \\ 4 & 5\end{array}\right]\left[\begin{array}{l}2 \\ 4\end{array}\right]+\left[\begin{array}{l}3 \\ 6\end{array}\right][6]} \\ {\left[\begin{array}{ll}7 & 8\end{array}\right]\left[\begin{array}{l}1 \\ 3\end{array}\right]+[9][5]} & {\left[\begin{array}{ll}7 & 8\end{array}\right]\left[\begin{array}{l}2 \\ 4\end{array}\right]+[9][6]}\end{array}\right]$

（本节来源于 https://zhuanlan.zhihu.com/p/133330692）

置换矩阵 Permutation matrix

有一种矩阵称为置换矩阵（Permutation matrix），它可以对矩阵进行行变换和列变换。如，我们要表示矩阵两行之间的交换，可以将置换矩阵左乘要变换的矩阵：

$\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix} \begin{bmatrix}a & b \\ c & d\end{bmatrix} = \begin{bmatrix}c & d \\ a & b\end{bmatrix}$

同理，对于列变换只需要右乘。

矩阵的逆

对于一个矩阵所表示的行初等变换，我们可以使用另一个矩阵来“恢复它的操作”，这样的矩阵是原矩阵的逆矩阵（Inverse matrix）。矩阵 $A$ 的逆矩阵记为 $A^{-1}$。自然，有 $A A^{-1} = A^{-1}A = E$.

矩阵何时有逆？不如讨论没有逆的情况。对于奇异矩阵（Singular matrix，即不满秩）或对应行列式等于 0 的矩阵）没有逆矩阵。因为它们中的向量共线，乘上另一个矩阵无法构成单位矩阵。

另一种理解是：对于方阵，如果存在非零向量 $x$ 使得 $Ax = 0$，那么矩阵也没有对应的逆矩阵。在等式两边同时乘 $A^{-1}$，左侧变为 $x$ 而右侧仍然为 $0$，但 $x \neq 0$，与命题相悖。

使用 Gauss-Jordan 消元求逆

当要求矩阵 $A$ 的逆时，在 $A$ 的右边放一个单位矩阵，我们称 $\begin{bmatrix}A & I\end{bmatrix}$ 为增广矩阵。对增广矩阵实施行初等变换，即左乘一个矩阵 $P$，如果使得 $P\begin{bmatrix}A & I\end{bmatrix} = \begin{bmatrix}PA & P\end{bmatrix} = \begin{bmatrix}I & P\end{bmatrix}$ ，则 $P$ 就是 $A^{−1}$.

现在要求一个矩阵 $\begin{bmatrix}1 & 3\\ 2 & 7\end{bmatrix}$ 的逆 $A^{-1}$，即：$\underset{A}{\begin{bmatrix}1 & 3\ 2 & 7\end{bmatrix}}
\underset{A^{-1}}{\begin{bmatrix}a & c\ b & d\end{bmatrix}}

\underset{E}{\begin{bmatrix}1 & 0\ 0 & 1\end{bmatrix}}$.

使用 Gauss-Jordan 法消元，将单位矩阵放到要求逆的矩阵右侧，得到一个增广矩阵：

$\begin{bmatrix} \begin{array}{cc | cc} 1 & 3 & 1 & 0\\ 2 & 7 & 0 & 1\\ \end{array} \end{bmatrix} \rightarrow \begin{bmatrix} \begin{array}{cc | cc} 1 & 3 & 1 & 0\\ 0 & 1 & 2 & 1\\ \end{array} \end{bmatrix} \rightarrow \begin{bmatrix} \begin{array}{cc | cc} 1 & 0 & 7 & -3\\ 0 & 1 & -2 & 1\\ \end{array} \end{bmatrix}$

• 将单位矩阵放到原矩阵的右侧
• 对第二行进行消元，消去 $(2, 1)$
• 再回代到第一行，消去 $(1, 2)$
• 右侧的矩阵就是矩阵 $A$ 的逆矩阵 $A^{-1}$，即 $\begin{bmatrix}7 & -3\\ -2 & 1\end{bmatrix}$.

如前述，矩阵本身表示了变换，矩阵的左乘表示对另一个矩阵的行变换。我们对矩阵 $A$ 进行的操作，也会原样地作用于右边的单位矩阵上。当左侧的原矩阵被化为单位矩阵时，右侧的单位矩阵也就变成 $A^{-1}$ 了。

参考资料

1. 【2.5】矩阵分块相乘 - 知乎
2. gauss_jordan法求矩阵的逆 - cnblogs
3. 三记的专栏 - CSDN