高等数学5 微分中值定理和导数的应用

微分中值定理

Fermat 定理

极值 若在点 $x_{0}$ 的邻域, 有 $f(x) \leq f(x_{0})$，称 $f\left(x_{0}\right)$ 是 $f(x)$ 的一个极大值, 称 $x_{0}$ 为 $f(x)$ 的一个极大值点 （类似地有极小值的概念）

定理 若 $f(x)$ 在点 $x_{0}$ 处取得极值, 且 $x_{0}$ 可导, 则 $f^{\prime}\left(x_{0}\right) = 0$。

Rolle 定理

若：(1) $f(x) \in C[a,b]$ (2) $f(x) \in D(a, b)$ (3) $f(a) = f(b)$

有：$\exists \xi \in (a, b), f'(\xi) = 0$

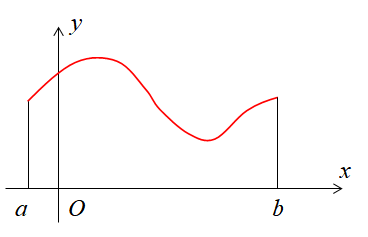
证明 （思路：是否有极值点）

由闭区间连续函数性质，$\exists x_1, x_2 \in [a,b]$, $f(x_1) = M = \max_{[a,b]} f(x)$, $f(x_2) = m = \min_{[a,b]} f(x)$.

1. 若 $x_1, x_2$ 均为 $[a, b]$ 端点，则 $M = m$，$f(x) = C$
2. 若 $x_1, x_2$ 至少有一个不与端点值相等，不妨设 $x_1$。此时 $M > f(a) = f(b)$，故 $x_1$ 为极大值点，由费马定理， $f'(x_1) = 0$.

Lagrange 定理

若：(1) $f(x) \in C[a,b]$ (2) $f(x) \in D(a,b)$

则： $\exists \xi \in (a, b), f'(\xi)= \frac {f(b) - f(a)}{b - a}$.

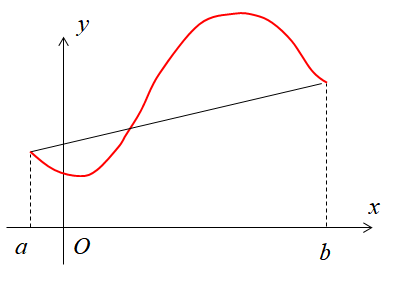
证明思路 （构造辅助函数）使曲线的开始和结束点水平，也就是将曲线方程减去直线的方程。为方便使用罗尔定理，改写结论：$f'(\xi) - \frac {f(b) - f(a)}{b - a} = 0$，这是一个导函数的值为 0，可看出构造的辅助函数为 $F(x) = f(x) - \frac{f(b) - f(a)}{b - a}x$。由于需要满足 $F(a) = F(b)$，在 $F(x)$ 中加个常数变成 $F(x) = f(x) - \frac{f(b) - f(a)}{b - a}(x - a)$ 即可。

证明 设 $F(x) = f(x) - \frac{f(b) - f(a)}{b - a}(x - a)$，由 $f \in C[a,b] \cap D(a,b) $ $\Rightarrow$ $F(x) \in C[a,b] \cap D(a,b)$

$F(a) = f(a)$, $F(b) = f(b) - f(a)$, 依据罗尔定理，存在一点 $\xi$，$F'(\xi) = 0$ $\Rightarrow$ $f'(\xi) = \frac{f(b) - f(a)}{b - a}$ ，证毕。

Lagrange 定理结论的另一形式

$a<\xi<b \Rightarrow 0<\frac{\xi-a}{b-a}<1$，记 $\theta=\frac{\xi-a}{b-a}$，则 $\xi=a+\theta(b-a)$, 从而定理的结论：$$\exists \theta \in(0,1)$$, $$f(b)-f(a)=f’a+\theta(b-a)$$

也描述为：

若取 $a=x, b=x+\Delta x$, 则 $\exists \theta \in(0,1)$, $f(x+\Delta x)-f(x)=f^{\prime}(x+\theta \Delta x) \Delta x$

推论

$f'(x)= 0 \quad (x\in I)$ $\Rightarrow$ $f(x) = c \quad(x \in I)$

1. 例： $a > 0$，求证 $\displaystyle \frac \alpha {1+\alpha} < \ln(1+\alpha) < \alpha$
2. 设 $\displaystyle \frac {a_0} {n+1} + \frac {a_1} {n} + \cdots + \frac {a_{n-1}} {2} + a_n = 0$，试证方程 $a_0 x^n + a_1 x^{n-1} + \cdots + a_{n-1}x + a_n = 0$ 在 $(0, 1)$ 至少有一个根
3. 设 $f(x) \in C[a, b] \cap D(a,b)$, $f(a) = f(b) = 0$，求证 $\exists \xi \in (a, b)$, $f'(\xi) = f(\xi)$.
4. 设 $f(x) \in C[a, b] \cap D(a,b)$, $f(a) = f(b) = 0$，试证 $\exists \xi \in (a, b)$, $\frac{f(\xi)}{\xi} = \frac{f'(\xi)}{2014}$.

Cauchy 定理

有：(1) $f(x), g(x) \in C[a,b]$ (2) $f(x), g(x) \in D[a, b]$ 且 $g'(x) \neq 0$

得：$\exists \xi \in(a, b)$， $\displaystyle \frac{f'(\xi_1)}{g'(\xi_2)} = \frac{f(b) - f(a)}{g(b) - g(a)}$

Cauchy 定理是 Lagrange 定理的推广，注意，不能对 $f, g$ 分别用 Lagrange 定理。证明思路：改写结论 $f'(\xi) = \frac{f(b) - f(a)}{g(b) - g(a)} g'(\xi)$ ，辅助函数 $f(x) - \frac{f(b) - f(a)}{g(b) - g(a)} (g(x) - g(a))$.

例：设 $f(x) \in C[a, b]$, $(0 < a < b)$，且 $f$ 在 $(a, b)$ 可导。试证 $\exists\xi\in (a,b)$，使得 $\frac {f(b) - f(a)}{b-a} = \frac{\xi^2 f'(\xi)}{ab}$

在图形上，Cauchy 定理和 Lagrange 定理一样。记参数方程 $y = f(t)$， $x = g(t)$，$\frac {dy}{dx} = \frac{f'(t)}{g'(t)}$.

L’ Hospital 法则

$\frac{0}{0}$ 型

有：(1) $\lim_{x\rightarrow a} f(x) = \lim_{x\rightarrow a} g(x) = 0$ (2) $f(x), g(x)$ 在 $a$ 点领域可导且 $g'(x) \neq 0$ (3) $\lim_{x\rightarrow a}\frac {f'(x)}{g'(x)} = A$

得：$\lim_{x\rightarrow a} \frac {f(x)}{g(x)} = A$. 意味着 $\frac 0 0$ 型的极限 $\lim_{x_\rightarrow a}\frac {f(x)}{g(x)} = \lim_{x_\rightarrow a}\frac {f'(x)}{g'(x)}$ 在右端有意义的情况下成立。

证明 （使用柯西定理）

补充定义 $f(a) = \lim_{x\rightarrow a}f(x) = 0$, $g(a) = 0$ $\Rightarrow$ $f(x), g(x)$ 在 $a$ 点连续, $[a, x]$ 或 $[x, a]$ 连续，且在 $(a, x)$ 或 $(x, a)$ 可导。

$\lim_{x\rightarrow a} \frac {f(x)}{g(x)} = \lim_{x\rightarrow}\frac{f(x) - f(a)}{g(x) - g(a)} = \lim_{\xi \rightarrow a}\frac{f'(\xi)}{g'(\xi)} = A$ （$\xi$ 在 $a$ 与 $\xi$ 之间，当 $x\rightarrow a$ 时 $\xi \rightarrow a$）

注意

• $x \rightarrow a^+$（或 $a^-$，$\infty$ 等）法则仍然适用
• 应用法则时，不要忘记等价无穷小替换
• $\lim_{x\rightarrow a}\frac {f'(x)}{g'(x)}$ 不存在不意味着 $\lim_{x\rightarrow a}\frac{f(x)}{g(x)}$ 不存在

$\frac{\forall}{\infty}$ 型

有：(1) $\lim_{x\rightarrow a}g(x) = \infty$ (2) $f(x), g(x)$ 在 $a$ 的领域可导且 $g'(x)\neq 0$ (3) $\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)} = A$ （$A$ 可以不存在，即为 $\infty$）

得：$\lim_{x\rightarrow a} \frac{f(x)}{g(x)} = A$

证明略。

Taylor 定理

泰勒公式考虑使用多项式逼近函数。

一点附近的 Taylor 公式

若 $f(x)$ 在 $x_0$ 附近有定义，且在 $x_0$ 有 $n$ 阶导数，则：

$f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+o\left(\left(x-x_{0}\right)^{n}\right)$

分析

我们记 $f(x) = f(x_0) + f'(x_0)(x - x_0) + a_2(x - x_0)^2 + a_3(x - x_0)^3 + \cdots$

对两边求导， $f'(x) = f'(x_0) + 2a_2(x - x_0) + 3a_3(x-x_0)^2 + \cdots$

再两边求导，$f''(x) = 2a_2 + 6a_3(x - x_0) + \cdots$

若左右两侧取 $x = x_0$，右边每一项 $x - x_0$ 就可以消去，所以 $a_2 = \frac{f''(x_0)}{2}$，$a_3 = \frac{f^{(3)}(x_0)}{3!}$ … 猜测 $a_n = \frac{f^{(n)}(x_0)}{n!}$

证明 （多次使用洛必达法则）

$P(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}$

结论即证明 $\lim _{x \rightarrow x_{0}} \frac{f(x)-P(x)}{\left(x-x_{0}\right)^{n}}=0$

求 $n - 1$ 阶导数，原式 = $\lim _{x \rightarrow x_{0}} \frac{f^{(n-1)}(x)-P^{(n-1)}(x)}{n !\left(x-x_{0}\right)} = \lim _{x \rightarrow x_{0}} \frac{f^{(n-1)}(x)-\left[f^{(n-1)}\left(x_{0}\right)+f^{(n)}\left(x_{0}\right)\left(x-x_{0}\right)\right]}{n !\left(x-x_{0}\right)} = \lim_{x\rightarrow x_0}\left[\frac{f^{(n-1)}(x) - f^{(n-1)}(x_0)}{n!(x-x_0)} - \frac{f^{(n)}(x_0)}{n!}\right] = \frac{f^{(n)(x)}}{n!} - \frac{f^{(n)(x_0)}}{n!} = 0$

注意，命题中 $f(x)$ 在 $x_0$ 处有 $n$ 阶导数，但 $x_0$ 点附近未必有 $n$ 阶导数。

区间 $(a, b)$ 上的 Taylor 公式

若 $f(x)$ 在 $(a, b)$ 有 $n + 1$ 阶导数，$x_0 \in (a, b)$ ，则在 $(a, b)$ 成立

$f(x)= f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots +\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{n}(x)$

其中，$R_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_{0}\right)^{n+1}$ （$\xi$ 在 $x, x_{0}$ 之间，可以记 $\xi = x_0 \pm \theta\Delta x$ ），通常称为皮亚诺（Peano） 余项。

分析 仍记 $P(x)$ 为前述的多项式，结论为 $\frac{f(x) - P(x)}{(x - x_0)^{n + 1}} = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}$

证明 可用 Cauchy 定理证明，求 $n$ 阶导数。

例：写出 $f(x) = x^2 \ln x$ 在 $x = 1$ 处的二阶 Taylor 公式

$f(0) = 1$

$f'(x) = 2x \ln x$ $f'(x) = 1$

$f'(x) = 2\ln x + 2 + 1$ $f''(x) = 3$

所以 $f(x) = x^2 \ln x = (x-1) + \frac3 2(x-1)^2 + o((x - 1)^2)$

如果要求写 Lagrange 余项，$f^{(3)}(x) = \frac 2 x$

$f(x) = x^2 \ln x = (x-1) + \frac3 2(x-1)^2 + o(\frac 3 \xi \cdot \frac{(x-1)^3}{3!})$

描述一点附近的函数情况，使用一点附近的泰勒公式，余项为比第 $n$ 项高阶的无穷小，在求极限的时候易得极限为 0，而在描述整体函数状况时需要使用区间的泰勒公式。在证明题一般要用区间上的泰勒公式。

常见函数的 Maclaurin 公式

对于函数 $f(x)$，$f(x)=f(0)+f^{\prime}(0) x+\frac{f^{\prime \prime}(0)}{2 !} x^{2}+\cdots+\frac{f^{(n)}(0)}{n !} x^{n}+R_{n}(x)$

$R_{n}(x)$ 为 Lagrange 余项 $\frac{f^{(n+1)}(\theta x)}{(n+1) !} x^{n+1}$ $(\theta \in(0,1))$，或 Peano 余项 $o\left(x^{n}\right)$。

1. $\displaystyle {\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+\cdots +x^{n}+\cdots$ （$\forall x:\left|x\right|<1$）（几何级数）

2. $\displaystyle e^{x}=1+x+\frac{x^{2}}{2 !}+\cdots+\frac{x^{n}}{n !}+\frac{e^{\theta x} x^{n+1}}{(n+1) !}$

3. $\sin x=x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}-\cdots+(-1)^{k-1} \frac{x^{2 k-1}}{(2 k-1) !}+\frac{\sin \left(\theta x+\frac{2 k+1}{2} \pi\right)}{(2 k+1) !} x^{2 k+1}$

4. $\displaystyle (1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}=1+\alpha x+{\frac {\alpha (\alpha -1)}{2!}}x^{2}+\cdots +{\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}x^{n}+\cdots$

5. $\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots +{\frac {(-1)^{n+1}}{n}}x^{n}+\cdots$ （$\forall x\in (-1,1]$）

1. 例：求极限 $\lim_{n\rightarrow \infty} n^2 (\sqrt[n]{a} - \sqrt[n+1]{a})$
2. 例：$f(x) = x e^x$
3. 例：$f(x) = \ln(2 - 3x + x^2)$
4. 例：设 $f(x)$ 在 $x = 0$ 的邻域二阶可导，且 $\lim_{x\rightarrow 0}\frac{\sin x + x f(x)}{x^3} = 0$，试求 $f(0)$, $f'(0)$ 和 $f''(0)$ 的值。
5. 例： $f(x)$ 在 $R$ 有二阶导数， $f''(x) > 0$，试证： $\forall x, h \in R$，$h\neq 0$：$f(x+h) + f(x-h) > 2f(x)$ （区间泰勒公式）

小结

应用 Taylor 公式主要在两类习题：

• 求极限，可用 Peano 余项形式
• 证明题，一般需要应用 Lagrange 余项形式

利用导数研究函数性态

判断单调性

$f(x)$ 在区间 $I$ 可导，则：(1) $f'(x) > 0$ $\Rightarrow$ $f(x)$ 在 $I$ 严格单调增加 (2) $f'(x) < 0$ $\Rightarrow$ $f(x)$ 在 $I$ 严格单调减小

• 若 $f'(x)$ 仅在 $I$ 内的孤立点为零，结论不变
• $I$ 为闭区间时，端点只要连续，结论不变
• 若 $f'(x) \geq 0$，结论中的的严格单调改为单调
• 逆命题不成立

1. 例：讨论函数 $f(x) = x^2 e^{-x}$ 的单调性

2. 例：试证当 $x>0$ 时，$\sin x > x - \frac {x^3}{6}$

   设 $f(x) = \sin x - x + \frac {x^3}{6}$，$f'(x) = \cos x - 1 + \frac {x^2}2 = \frac{x^2}2 - 2\sin^2 \frac x 2 = 2\left((\frac x 2)^2 - (\sin^2\frac x 2)\right)$ ，所以 $f(x)$ 严格单调增加。当 $x>0$，$f(x) > f(0) = 0$ ，$\sin x > x - \frac {x^3} 6$

3. 例：试证 $\forall a, b > 0$，$ae^{2a} + be^{2b} \geq (a+b)e^{a+b}$ 成立

   可以构造辅助函数 $F(x)$ 或将式子变形并证明。

判断极值

导数为 0 的点称为驻点。$f(x)$ 的极值点应为驻点或导数不存在的点。

极值第一判别法：

$f(x)$ 在 $x_0$ 连续且在其去心邻域内可导，则

• 当 $f'(x)$ 在 $x_0$ 左正右负，$x_0$ 是 $f(x)$ 的极大值点
• 当 $f'(x)$ 在 $x_0$ 左负右正，$x_0$ 是 $f(x)$ 的极小值点
• 当 $f'(x)$ 在 $x_0$ 左右两侧同号，$x_0$ 不是 $f(x)$ 的极值点

1. 例：讨论 $f(x) = x^{\frac 2 3} (x+1)$ 的单调性和极值
2. 例：$a, b, p, q$ 均为正实数，且 $\frac 1 p + \frac 1 q = 1$，试证 $Young$ 不等式：$ab \leq \frac{a^p}{p} + \frac{b^q}{q}$

极值第二判别法：

$f(x)$ 在 $x_0$ 有二阶导数，$f'(x_0) = 0$，则：

• 当 $f''(x_0) < 0$ 时，$f(x)$ 在 $x_0$ 取最大值
• 当 $f''(x_0) > 0$ 时，$f(x)$ 在 $x_0$ 取最小值

1. 例：试求函数 $f(x) = e^x \cos x$ 在 $(0, 2\pi)$ 上的极值
2. 例：$y = a\sin x + \frac 1 3 \sin 3x$ 在 $x = \frac \pi 3$ 取得极值，求 $a$。此极值是极大值还是极小值？
3. 例：$y = y(x)$ 由方程 $2y^3 - 2y^2 + 2xy - x^2 = 1$ 所确定，求其极值。
4. 例：$f(x)$ 在 $\mathbf R$ 有二阶导数，$f''(x) > 0$，试证 $\forall x, h \in \mathbf R (h\neq 0)$： $f(x+h) + f(x-h) > 2f(x)$
5. 例：$x > 0$ 时，方程 $kx + \frac 1 {x^2} = 1$ 有且仅有一根，求 $k$ 的值。

最值的求法

连续函数 $f(x)$ 的最值点应为极值点或区间的端点。

1. 例：求 $f(x) = \sqrt[3]{(x^2 - 2x)^2}$ 在 $[-2, 3]$ 的最大最小值
2. 例：求 底面半径为 2cm 高为 3cm 的正圆锥内接长方体的最大体积

当可导函数在定义区间仅有惟一驻点时，而问题又显然有解且不可能在端点达到，则此驻点必为所求最大（小）值点。

凹凸性和拐点

凹凸性 $f(x)$ 在区间 $I$ 连续，且 $\forall x_1, x_2 \in I$, $a\in (0, 1)$ 有 $f(ax_1 + (1-\alpha)x_2) \leq \alpha f(x_1) + (1-\alpha)f(x_2)$，则称 $f(x)$ 在 $I$ 是下凸的，也称函数曲线在 $I$ 是下凸的，割线在曲线的上方。类似地，有上凸的概念。

式中如果是小于号且 $x_1 \neq x_2$ 时，称 $f(x)$ 严格下凸。

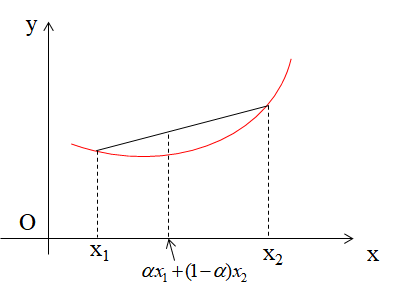
凸性第一判别法

若 $f(X) \in D(a, b)$，则

1. $f'(x)$ 严格单调增加时， $f(x)$ 在 $(a, b)$ 严格下凸
2. $f'(x)$ 严格单调减少时， $f(x)$ 在 $(a, b)$ 严格上凸

凸性第二判别法

若 $f(X)$ 在 $(a, b)$ 二阶可导，则

1. $f''(x) > 0$ 时， $f(x)$ 在 $(a, b)$ 严格下凸
2. $f''(x) < 0$ 时， $f(x)$ 在 $(a, b)$ 严格上凸

拐点 $f(x) \in C(a, b)$，$x_0 \in (a, b)$ 是 $f(x)$ 下凸与上凸的分界点，则称 $x_0$ 是函数$f$ 的拐点，而称 $(x_0, f(x_0))$ 为曲线 $y = f(x)$ 的拐点。

拐点的判别：连续函数 $f(x)$ 在 $x_0$ 处二阶导数为零（或不存在），则

1. $f''$ 在 $x_0$ 两侧异号时，$x_0$ 是 $f(x)$ 的拐点
2. $f''$ 在 $x_0$ 两侧同号时，$x_0$ 不是 $f(x)$ 的拐点

1. 例：设 $f(x) = e^{-x^2}$，试讨论其凸性与拐点
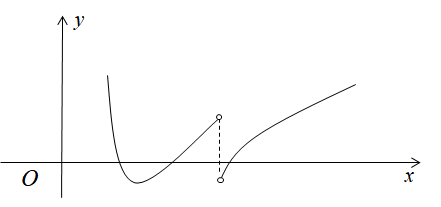
2. 例：已知 $f(x)$ 在 $\mathbf R$ 连续，$f'(x)$ 的图形如下，试求 $f(x)$ 的极值点和拐点数（四个极值点，一个拐点）。

3. 例：试证对 $\forall a, b > 0$ 成立，$\displaystyle a^a b^b \geq (\frac{a+b}{2})^{a+b}$

   对于幂指函数先取对数，再变形，找出辅助函数

函数的作图

曲线的渐近线

设 $P$ 是曲线 $C$ 上的一点，$O$ 是原点，$L$ 是一条直线。若 $\displaystyle lim_{OP\rightarrow +\infty} d(P, L) = 0$，其中 $d(P, L)$ 是 $P$ 到 $L$ 的距离，则称 $L$ 是 $C$ 的渐近线。

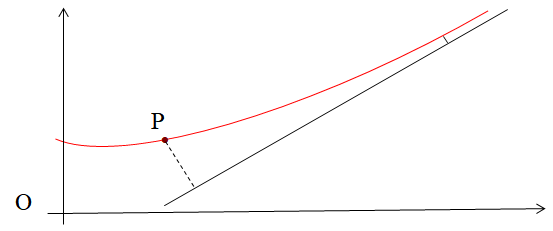
铅直渐近线

若 $\displaystyle\lim_{x\rightarrow x_0^+} f(x) = \infty$，则直线 $x = x_0$ 是曲线 $y = f(x)$ 的铅直渐近线。$x\rightarrow x_0^+$ 也可为 $x\rightarrow x_0^-$，表明曲线在渐近线的哪一侧。

例：讨论函数曲线 $y = \frac{x^3-2x+1}{x^2-1}$ 的铅直渐近线

水平渐近线

若 $\displaystyle\lim_{x\rightarrow +\infty} f(x) = b$，则直线 $y = b$ 是曲线 $y = f(x)$ 的水平渐近线。$x\rightarrow +\infty$ 也可为 $x\rightarrow -\infty$，表明曲线在何方向接近渐近线。

例：讨论 $\displaystyle\frac{\sqrt{x^2}}{x-1}$ 的水平渐近线

斜渐近线

如果 $y = ax+b$ 是曲线 $y = f(x)$ 的斜渐近线，则 $\displaystyle\lim_{x\rightarrow +\infty} [f(x) - (ax+b)] = 0$ （或 $x\rightarrow -\infty$）$\Rightarrow$$\displaystyle\lim_{x\rightarrow+\infty}\frac{f(x)}{x} = a$, $\displaystyle\lim_{x\rightarrow+\infty}[f(x) - ax] = b$

1. 例：$\displaystyle y = \frac{x^3}{x^2-2x-3}$
2. 例：$y = f(x)$ 是 $y^3 - x^3 + 2xy = 0$ 的隐函数，曲线 $y = y(x)$ 存在斜渐近线，试求之。

函数图形的描绘

• 讨论函数 $f(x)$ 的定义域、奇偶性、周期性
• 求出导数 $f'$，$f''$，确定 $f$ 的间断点和 $f'$，$f''$ 为零或不存在的点
• 以上述点将定义域分成若干区间，通过列表讨论单调性、极值、凸性和拐点
• 求出渐近线
• 描绘图形，有时可取图形上几个特殊点

例：考察函数的性态且作图： $y = \frac{x|x|}{1+x}$

平面曲线的曲率

弧长与微分

弧长

弧长指的是曲线内接折线长度的极限（组成折线的线段长 → 0）。设曲线 $C: y=f(x), x\in [a, b]$，其上 $P_0$, $P$ 分别对应 $x_0$, $x$，记弧长 $\widehat {P_0P} = S(x)$ ，由 $\Delta x$ 产生 $\Delta x$，有：（1）$\Delta x$ 与 $\Delta s$ 同号 （2）$\displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta s}{PP'} = 1$

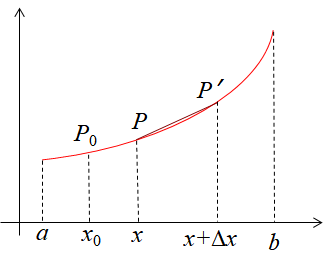
从而导出 $\displaystyle \frac{ds}{dx} = \sqrt{1+f'^2(x)} \Rightarrow ds = \sqrt{1 + f'^2(x)} dx$，在 $ds > 0$ 时，$ds = \sqrt{(dx)^2 + (dy)^2}$ 的几何意义是：微小弧长可由该处相应小切线段长代替

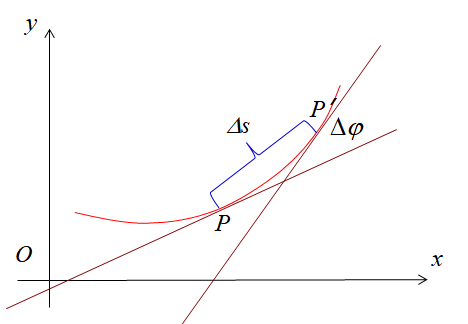
曲率

若曲线上 $P \rightarrow P'$ 对应的切线转动角度为 $\Delta \varphi$，对应弧长增量 $\Delta s$，定义 $\widehat {PP'}$ 的平均曲率为 $\frac{|\Delta \varphi|}{\Delta s}$

曲率 $k = \lim_{P'\rightarrow P} \frac{\Delta \varphi}{\Delta s} \Rightarrow k = |\frac{d \varphi}{d s}|$

定义曲率半径 $R = \frac 1 k$，曲率圆为曲线上某点 $P$ 指向凹侧的法线上到 $P$ 距离为 $R$ 的点为心，$R$ 为半径的圆。

曲率公式

若曲线上对应 $x$ 的 $P$ 点处切线的倾角为 $\alpha$，则 $\Delta \varphi = \Delta \alpha$ $\Rightarrow$$k = |\frac{d\varphi}{ds}| = |\frac{d\alpha}{ds}|$ $\Rightarrow$ $l = \left|\frac{y''}{(1 + y'^2)^{\frac 3 2}}\right|$

例：

1. 求曲线 $y=x^{2}+p x+q$ 上任一点的曲率
2. 求曲线 $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ 上点 $\left(\frac{a}{\sqrt{2}}, \frac{b}{\sqrt{2}}\right)$ 的曲率半径
3. 求曲线 $\left\{\begin{array}{l}x=x(t) \\ y=y(t)\end{array}\right.$ 上对应 $t$ 的点处的曲率
4. 求螺旋线 $r = a \theta$ 上对应 $\theta$ 的点处的曲率（改写成参数方程）